Dag Hofoss
Et sentralt ledd i gjennombruddsmetoden er ideen om å gjøre små lokale utprøvinger av forbedringsideer. «See what you can achieve by next Thursday» står det på t-skjortene som IHI har brukt til å promovere spredningen av denne måten å drive kvalitetsforbedringsarbeid på, og «Demings sirkel», se figur 10, ble, i Norge som i USA og Sverige, brukt som bilde på hvordan prosessen skulle rulle oppover kvalitetsforbedringsbakken ved gjentatte små omdreininger av hjulet hvis omkrets var delt inn i «Plan», «Do», Study» og «Act».
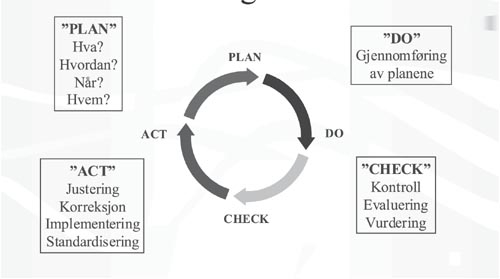
Figur 10. Demings sirkel.
En av erfaringene fra det første gjennombruddsprosjektet, og for den saks skyld også fra de to neste, var at helsepersonell ikke uten videre lot seg overbevise om at småskalaeksperimenter var en god ide. Det stanset ikke prosjektene. Det er ingen forutsetning for kvalitetsforbedring at en kartlegger endring og utvikling i henhold til en bestemt systematikk, og både i Gjennombruddsprosjektet Keisersnitt og Gjennombruddsprosjektet Intensivmedisin ble oppnådd gode resultater av avdelinger som ikke adopterte denne monitoreringsteknikken. Den sentrale prosjektledelsen ble likevel slått av misforholdet mellom prosjektets grunnleggende terminologi og formen på det lokale forbedringsarbeid i mange av de deltakende avdelinger. I prosjektets samlinger (FS 1, 2 og 3) og overfor og gjennom prosjektets veilederkorps ble det lagt betydelig vekt på at en nyttig vei å gå var småskalautprøvinger «by next Thursday». Av rapportene fra de deltakende avdelinger, og kanskje enda mer av de uformelle samtaler under prosjektsamlingene, var det imidlertid tydelig at en lokalt ikke var like opptatt av «Demings sirkel». Det var ikke noe alarmerende problem, for mange avdelinger gjorde store framsteg i retning av de mål de hadde satt seg. Men det reiste først spørsmålet om hvorfor er helsearbeidere ikke så opptatt av småskalaeksperimenter, og dernest spørsmålet hva skal eventuelt til for å vekke deres lyst til slikt.
Etter en stund gikk det opp for oss at mange oppfattet «Demings sirkel» som et ord i kvalitetsforbedringsliturgien. Og travle helsearbeidere er ofte ikke velvillig innstilt overfor ny sjargong, de ønsker nye og bedre løsninger, ikke mer moderne ord. Kvalitetsforbedringsspråket er, i den grad det bare er ny terminologi, snarere et hinder enn en hjelp - slik figur 11 antyder.

Figur 11. En kvalitetssforbedringsarbeiders skjebne.
Det er lett å forstå at «Demings sirkel» kan framkalle en slik reaksjon. For hva annet er den, enn ny flaske til gammel vin - et nytt navn på hypotetisk-deduktiv metode, som ikke ble oppfunnet av vår tids kvalitetsforbedringsekspert Walter Edwards Deming, men har vært vitenskapens grunnprinsipp siden Aristoteles? «Slik har vi alltid gjort», kan helsepersonell si, og med full rett: på bakgrunn av vår erfaring danner vi oss hypoteser, vi prøver dem ut, aksepterer eller forkaster dem - og tenker gjennom problemene ut fra kunnskap vi dermed har ervervet. Slik gjør vi når vi forsker, og slik gjør vi i det daglige, når vi f.eks. justerer enkeltpasienters medisinering, og vi trenger ikke lære det på nytt, under en ny overskrift.
Den andre grunnen til at helsepersonell ikke uten videre lar seg engasjere i småskalaforsøk er at en har lært at en må ha ganske store datasett for å kunne trekke statistisk sikre slutninger. Både i khikvadrattesting av forskjeller mellom fordelinger og i t-testing av forskjeller mellom gjennomsnitt er det slik at skal risikoen for å tro på en utvalgstilfeldighet være mindre enn 5 prosent, må antallet observasjoner være et ganske stort tall - mye større enn hva en rekker å observere «innen neste torsdag».
Gradvis gikk det opp for oss i den sentrale prosjektledelsen at vi måtte supplere påminnelsene om Deming med å fortelle om en type stat istisk analyse som ikke er mye brukt i helsetjenesten, men som er en viktig del av det statistisk-matematiske armamentarium i mange andre fag, nemlig tidsserieanalyse. Det har vi derfor gjort, både i Gjennombruddsprosjektet Intensivmedisin og enda mer i Gjennombrudds-prosjektet Psykiatri. Vi har inkludert slik demonstrasjon i plenumsforedrag under forbedringsseminarene, og veilederkorpset har hatt egne samlinger med det som tema.
Og resultater av det avtegner seg over tid i prosjektene. Mens rapportene fra de deltakende avdelingene i Gjennombruddsprosjektet Keisersnitt så å si ikke inneholdt referanser til slike teknikker, dukket de opp i rapportene fra intensivavdelingene, og enda mer fra avdelingene som deltok i Gjennombruddsprosjektet Psykiatri.
Tidsserieanalyse og statistisk prosesskontroll
Når oppgaven er å studere resultater over tid, er den naturlige løsning å bruke en metode som er laget nettopp for det formålet. Det finnes mange teknikker i den familien. De har alle samme etternavn: tidsserieanalyse.
Om tidsserieanalyse finnes en stor litteratur. Figur 12 viser en side fra en bok om tidsserieanalyse, for å «føre bevis for» at det faktisk finnes slike metoder.
Figur 12. Fra McDowell D, McCleary R, Meidinger EE, Hay RA jr.. Interrupted Time Series Analysis. London: Sage 1980.
Og det er kanskje behov for å føre sannhetsbevis for det, for tidsserieanalyser er ikke mye brukt i helsetjenesten. Tidsserieanalyse er utviklet i andre vitenskaper, nemlig i fag som studerer sykluser som ingen vet hva kommer av, nemlig i økonomien (konjunkturer) og meteorologien (klimasvingninger). Hvis en tror at markedet er en selvstendig kraft som selv produserer konjunktursvingninger eller hvis en ikke ønsker å tro at den globale temperaturøkingen skyldes noe som menneskene har gjort, ja, da må vi predikere utviklingen ut fra observasjonsseriens iboende mønster. En parallell fra helsetjenesten er at det kan hende at det er bortkastet tid å forsøke å tilbakeføre pasienttilfredshet til kjennetegn ved pasienter, som alder, utdanning, inntekt og kjønn («det er de unge, de middels høyt utdannete, de trekvart rike og kvinnene som er misfornøyd»), for det kan hende at pasienttilfredshet går i konjunkturbølger. Vi er så å si inne i vår misnøyes vinter - men etter vinter kommer vår, det vet vi, for det har det alltid gjort før. I så fall er det bortkastet tid å forsøke å predikere framtida ut fra regresjonslikninger der de uavhengige variablene er endringer i pasientunderlagets alder, utdanning, inntekt og kjønn, i stedet bør en studere tilfredshetssvingningene med tanke på å avdekke deres iboende dynamikk, dvs deres mønster.
Hovedtyngden av tidsserieanalyselitteraturen handler om identifiseringen av fasongen på autoregressive integrerte prosesser med bevegelige gjennomsnitt, f.eks. ad modem Box-Jenkins: ARIMA-analyse (av AutoRegressive Integrerte tidsserier med Moving Averages): er prosessen autoregressiv, er den integrert, og har den bevegelig gjennomsnitt, og hvilken formel følger den da?
Men det finnes også en enklere slektning: statistisk prosesskontroll, SPC. I vår sammenheng innebærer det at en legger merke til et problem, planlegger et forbedringstiltak, iverksetter den planlagte intervensjonen og studerer endringene i den første perioden etter at forbedringen ble gjort,. dvs gjennomfører et lite eksperiment, og registrerer resultatobservasjonene over tid, dvs plotter dem langs tidsaksen i stedet for å slå dem sammen i to grupper med overskriften «Før» og «Etter». Slagordet i statistisk prosesskontroll er da også (TRSP: Plot the dots!) «Plot the dots!»
Helsepersonell er vant til at det skal temmelig mange observasjoner til før en kan våge å bygge beslutninger på dataene. Men det gjelder ikke hvis observasjonene utgjør en tidsserie. Ordet «påhverandrefølgende» innebærer viktig tilleggsinformasjon. En kan nemlig trekke statistisk sikre konklusjoner på grunnlag av ganske få observasjoner dersom observasjonene utgjør en tidsserie. En sett av observasjoner som er gjort etter hverandre med jevne mellomrom er noe helt annet og mer informativt enn en gruppe observasjoner som er gjort samtidig. Sett at en prosess har en kjent og stabil medianverdi - f.eks. at medianen for den andel av pasientene som sa seg svært fornøyd med oppholdet i avdelingen for ukene i de siste tre årene er 60 %. Plottet uke for uke var det naturligvis variasjon, noen uker var det mer enn 60, andre uker mindre. Men plottet viser en stabil prosess som svinger omkring et bestemt nivå. Så gjør vi en intervensjon: vi melder tilbake til avdelingen hva pasientene sier om denne og andre avdelinger. Uka etter ligger prosenten over 60. I en stabil prosess er sannsynligheten for dét 50 % (det kan like gjerne svinge litt opp som litt ned), så det ligger ikke noe viktig signal i det. Også neste uke ligger skåren over prosessens tidligere medianverdi. Men i en stabil prosess er sannsynligheten for to påhverandrefølgende uker over medianen ½* ½ = 25 %, så det er ikke noe viktig signal i det heller - og heller ikke i at verdien i uke 3 også ligger over medianen: ½* ½*½ = 12,5 %, så fortsatt er her ikke noe signal. En kan heller ikke i uke 4 våge å tro på en forbedring, for fire gode uker på rad vil skje i (½)4 = 6,25 % av tidsserieobservasjonene av en prosess der ingen endring har skjedd. Men sannsynligheten for å observere en prosentandel over medianen fem uker på rad er bare (½)5 = 3,125 % om prosessen er stabil. Dermed har vi et statistisk sikkert signal om endring i prosessen: pasientene ser faktisk ut til å ha blitt mer fornøyd (p < ,05). Og nøkkelen til å oppdage signalet i så få observasjoner er å se at konsekutive observasjoner er noe annet enn samtidige tverrsnittsobservasjoner.
Kanskje trenger en litt flere. Vil en ikke løpe så stor risiko som 5 % for å tro på en tilfeldighet, men maksimalt 1 %, må en ha sju på rad over gjennomsnittet (for ½7 = 0,0078125, dvs under 0,01), og vil en ikke løpe større risiko enn 5 promille, må en ha åtte på rad (for ½8 = 0,00390625, dvs under 0,005).
Men det er viktig å holde fast ved en ikke kan si statistisk sikkert at en har oppdaget en endring i en prosess uten at en har minst fem oppfølgingsobservasjoner. Enda vanligere enn å være for sein til å se signalet i en tidsserie er nemlig å være for rask. De to feilene (overforsiktighet, type 2-feil, og godtroenhet, type 1-feil) er så å si forankret i hver sin rolleposisjon i helsetjenesten: forskere krever ofte for store materialer («En kan ikke trekke slutninger når vi ikke har flere observasjoner enn de vi rekker å få i dette korte prosjektet»), ledere reagerer ofte på for små materialer («Nå går det dårligere enn før - jeg må skynde meg å gjøre noe»).
Det er nemlig mange som synes de ser trender der ingen kan vite om det finnes noen. Det er vanlig når en snakker om nasjonaløkonomien: «I forrige kvartal var overskuddet på handelsbalansen 900 millioner, i dette kvartalet var det bare 400 - så nå går det raskt utforbakke». Men om de to punktverdiene hørte hjemme i en tidsserie der en alltid hadde vekslet mellom et overskudd på mellom 100 millioner og 1000 millioner, var det ingen grunn til alarm - heller ikke om overskuddet pleide å svinge om 200 millioner.
Skal en unngå å se spøkelser, men samtidig oppdage de signaler som finnes i små datasett ordnet over tid, må en vite om de formelle teknikker som finnes for å analysere tidsrekker. De er altså to: tidsserieanalyse og statistisk prosesskontroll. Her ikke tid/sted til å si mer om tidsserieanalyse. Men jeg skal forsøke å gi en intuitiv forståelse av hva statistisk prosesskontroll er, og et par smakebiter.
Utgangsideen er begrepet «naturlig variasjon». Alle prosesser, også de helt stabile, er kjennetegnet av naturlig variasjon, og oppviser litt ulike verdier på ulike tidspunkter. Fordi alt styres/påvirkes av en lang rekke faktorer vil prosessresultater fordele seg «nokså normalt». Å kjøre til jobben, f.eks., tar som oftest normalt lang tid. Men noen ganger går det utrolig greit (liten trafikk, bare grønne lys), andre ganger tar det håpløst lang tid (alle kjører samtidig med oss, bare røde lys, damer får motorstopp og menn med hatt kolliderer etc etc). Slike dager har et spesielt navn: «The Day from Hell». De er fryktelige, men de gir ingen grunn til angst for at nå går det nedover. Vi vet jo at det ikke er fordi vi er blitt dårligere til å kjøre at turen tok så lang tid i dag: kjøretiden er bare et uttrykk for prosessens normalvariasjon. I statistisk prosesskontroll kalles det også for «common cause»-variasjon. Den skyldes, som navnet sier, et sett av faktorer som er til stede hele tida. Noen av dem trekker oppover, andre nedover, og noen ganger er de som trekker oppover litt sterkere, andre ganger dominerer de som drar nedover. Derfor svinger prosessverdiene opp og ned - men så langt variasjonen bare er «common cause variation», vil den svinge omkring et gitt nivå.
Alle prosesser har sin normalvariasjon. Den kan identifiseres. Ofte kalles den for «prosessens stemme», eller «kapabilitet». Og det er prosessens stemme som er utgangspunktet for alt vettugt forbedringsarbeid. Å gripe inn i en prosess fordi en er misfornøyd med en måleverdi (eller to, eller tre, eller fire) betyr ofte at en forsøker å rette på noe som grunnleggende sett er i orden. «Tampering» heter det i den engelskspråklige litteraturen om statistisk prosesskontroll - på norsk kunne det kanskje kalles klåing.
For husk: en må observere minst fem fallende (eller synkende) verdier på rad for å kunne snakke om en trend. For er prosessen stabil, kan neste verdi like gjerne ligge over som under den sist målte. Men å tro at to synkende verdier på rad betyr en negativ trend, er å løpe en risiko på 25 % for å ta feil. Resonnementet som viser det, er det samme som over. Å tro at tre stigende (eller synkende) verdier på rad signaliserer en trend, er å løpe en risiko på 12,5 % for å ta feil osv. Minst fem må til. Og vil en ikke løpe større risiko enn én prosent for å gjøre en type 1-feil og tro på en trend som bare var en tilfeldighet, må en, parallelt med det vi sa over, ha sju på rad.
Det er ofte fristende å mene at en har oppdaget at en prosess forverrer seg. Men det er viktig å unngå å tro at en ser endringer der det i virkeligheten bare er normal fluktuasjon rundt et stabilt gjennomsnitt, både når en behandler pasienter og når en administrerer helsetjenestesystemer.
Ut fra egen erfaring vet vi at «The Day from Hell» kan ramme den beste. En viktig generalisering er at det også hender andre. Ut fra den erkjennelse kan en som leder unngå fristelsen til å klå på prosesser som er i orden, og dermed spare arbeidsplassen for omkostninger og seg selv for ubehag.
Klåing har nemlig regelmessig to slags uheldige konsekvenser. For det første kan over-årvåkenhet slite en helt ut. Et berømt - og i statistisk prosess kontroll-folkloren nærmest klassisk - eksempel er Demings kvalitetssikringsarbeid i en papirfabrikk i New Hampshire. Den vanskeligste biten av prosessen var glansingen av papiret. Det ble aldri helt bra, fort var papiret for blankt, for matt, for grovt, for ujevnt osv. Maskinen hadde mange ratt, og operatøren skrudde på dem så han ble svett, men uten varig suksess, og etter formiddagens serie med «finjusteringer» var mannen både utslitt og nedstemt. Demings løsning var å be mannen sitte rolig mens hans plottet variasjonen i papirkvalitet. Det overraskende resultatet var at variasjonen ble mindre når operatøren ikke justerte maskinen hele tida. Maskinen ga rett og slett slike resultater, det var slik den var. Så lenge glansingen foregikk ved hjelp av denne teknologien, ble resultatet slik. Løsningen var ikke større innsats, det som må til, er en ny framstillingsmåte, en endret prosess.
For det andre kan prosess-klåing skade samarbeidsklimaet. Ofte tar klåingen form av at medarbeidere refses for uheldige resultater som de ikke kunne rå med, men som uttrykker prosessens naturlige variasjon, dens stemme. Spissformulert er poenget at enhver prosess er perfekt designet for å gi nøyaktig de resultater den faktisk gir. Av og til skyldes dårlige resultater naturligvis slurv eller udugelighet. Men stort sett er produksjonsresultatene er prosessens stemme. Og folk reagerer når sjefen refser dem for dårlige resultater som egentlig bare er tilfeldig variasjon i en stabil prosess. De reagerer ulikt: noen aksepterer skrapen, blir nedfor og mister selvtillit, andre blir kontrære, mer eller mindre varig. Men begge typer reaksjoner er en unødig kostnad i produksjonsprosessen.
Dessuten avstedkommer klåingen mer direkte produksjonstap. Noe medisinsk-teknisk utstyr (film, legemidler) må oppbevares kjølig. I juli registrerer sykehuset mange feil som kunne ha kommet av at slike redskap ikke fungerte. Direktøren innkaller avdelingssjefen, som ikke har noen god forklaring. Og det er ikke rart, for det er ingen forklaring, det var ikke en gang noe som krevde forklaring - det var bare prosessens stemme som var slik, resultatene i juli var dårligere enn vanlig, men innenfor prosessens normalvariasjon. Men så er det det at på et så høyt sjefsnivå må møter gi forklaringer. De enes derfor om at kjølelageret nok ikke var kaldt nok, og driftssjefen får beskjed om å kontrollere det. Det er bortkastet tid: han finner ingen feil, for det var, som sagt, ingen feil. Men for sikkerhets skyld (eller av andre grunner, f.eks. fordi han lenge har ønsket en anledning til akkurat det) skifter han fustasjopphengsforkoblingen som han aldri har fått penger til på driftsbudsjettet. Og det verste er at det blir aldri oppdaget at det var bortkastet. «Mirakuløst» viser det seg nemlig at i neste måned er feilene færre - for slik er naturli g variasjons vesen: verdiene går opp og ned, selv i en stabil prosess. Men bortkastet var det likevel.
Et annet berømt anekdotisk eksempel er beretningen om flyvåpenobersten som av prinsipp refset alle som landet med et hump. Og han kunne glede seg over å få bekreftet sin pedagogiske teori hver gang: refs må være effektivt, for nesten ingen gjorde to ekstremt dårlige landinger på rad. Ros, derimot, er feilslått, for den som fikk skryt for en eksepsjonelt jevn landing, klarte nesten aldri å lande så fint neste gang. Men regresjon mot middelverdien er naturlig variasjons vesen og stabile prosessers stemme.
Hvordan finner en så prosessens stemme? Hvordan identifiserer en de trendtilløp og verdier som varsler at her er det ikke bare naturlig variasjon, men at noe spesielt er på ferde?
Det gjør en ved å tegne diagrammer der en plotter observasjonene over tid («Plot the dots!»). Diagrammene er av to hovedtyper: run-diagrammer og kontroll-diagrammer.
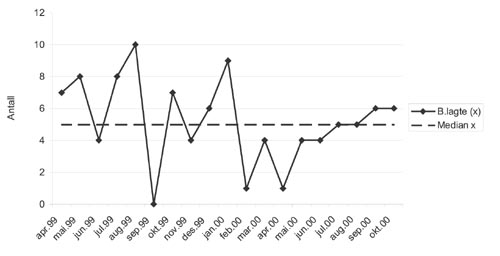
Et run-diagram er, som vist i figur 13, et tidsserieplott som viser observasjonsrekka og dens medianverdi.
Figur 13. Run-diagram. Antall beltelagte pasienter pr. måned. Markering av punktverdier og median.
Medianen er verdien til den observasjon ligger midt i den rangordnete fordeling av observasjoner, slik at den ene halvparten av observasjonene har lavere verdier, den andre halvparten høyere. Dersom antallet observasjoner er et likt tall, er ingen enkeltobservasjon i midten, men da ligger medianen midt mellom verdien til den øverste observasjonsverdien i nederste halvdel og den laveste observasjonsverdien i øverste halvdel. Et talleksempel gjør det tydelig. Om vi hver uke i ti uker har observert andelen tilfredse pasienter, kan tallene se ut som i tabell 1.
| Uke 1 | Uke 2 | Uke 3 | Uke 4 | Uke 5 | Uke 6 | Uke 7 | Uke 8 | Uke 9 | Uke 10 |
| 72 | 78 | 69 | 71 | 66 | 70 | 66 | 73 | 76 | 74 |
I rekka av prosenter er de fem laveste verdiene 66, 66, 69, 70 og 71 og de fem høyeste 72, 73, 74, 76 og 78. Medianverdien blir dermed (71+72)/2 = 71,5.
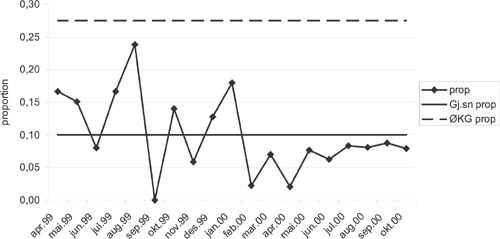
Et kontroll-diagram inneholder, som vist i figur 4, observasjonsrekka, dens gjennomsnittsverdi og øvre og nedre kontrollgrense, dvs grensene for normalvariasjonen i den observerte prosessen.
Figur 14. Kontroll-diagram. Andel (proportion) pasienter behandlet med fysiske tvangsmidler. Markering av punktverdier, gjennomsnitt og øvre kontrollgrense (ØKG).
Mens det bare finnes en type run-diagram, er kontrolldiagrammer av ulike typer, etter dataenes art. Det fører for langt å gå inn i det i denne artikkelen, så vi skal her bare se på de to enkleste. Det aller enkleste er XmR-diagrammet, som er det mest anvendelige, i den forstand at en alltid kan bruke det - de andre typene fordrer at dataene er av bestemte slag. Det andre eksemplet er p-diagrammet, som en anvender når en studerer endringer over tid i prosentandeler.
Run-diagrammer
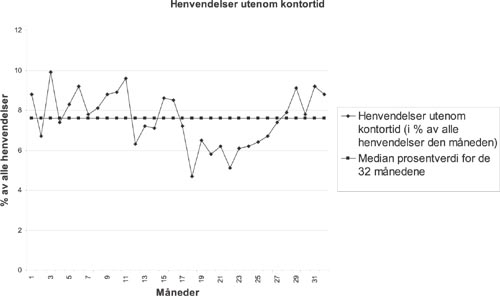
Figur 15 viser telefonhenvendelser utenfor kontortid til legekontoret i en kommune, plottet over 32 måneder, i prosent av alle henvendelser til legekontoret. I måned 17 iverksatte kommunen et tiltak som den håpet skulle redusere antallet unødige oppringninger om kvelden og natta: den delte ut til alle husstander et egenomsorgshefte som forklarte hvilke vanlige skader og sykdommer som ikke krevde øyeblikkelig legehjelp, men godt kunne vente til legekontoret åpnet neste dag. Spørsmålet er om run-diagrammet gjør det rimelig å forkaste nullhypotesen om at vi har å gjøre med en stabil prosess som bare oppviser tilfeldig variasjon rundt et bestemt nivå.
Figur 15. Telefonhenvendelser til legekontoret etter stengetid.
To tester på om run-diagrammer viser mer enn normal fluktuasjon rundt et gitt nivå er 1) om det inneholder «for lange» runs, og 2) om det inneholder for mange stigende (eller synkende) verdier på rad.
Den første testen («For lange runs?») sjekker om det har foregått et nivåskift (permanent eller midlertidig). Dersom vi ser en lang run, så må det ha vært noe som har holdt verdien fast over (eller under) medianen gjennom lang tid. Tilfeldig variasjon omkring et fast nivå vil innebære at observasjonene svinger omkring medianen, og ikke ligger spesielt lenge over (eller under) den av gangen.
Hva betyr så «for lang»? Carey & Lloyd (2001) gir svaret i form av tabell 2, som viser hvordan det avhenger av hvor mange observasjoner en har. «Brukbare» observasjoner er observasjoner som ikke ligger på medianen. En observasjon som ligger akkurat på medianen avbryter ikke en run, men forlenger den heller ikke, den skal rett og slett ikke telles med.
| Antall brukbare observasjoner | Hva er «for langt»? |
| Under 20 | Runs på 7 eller flere |
| 20 eller flere | Runs på 8 eller flere |
Run-diagrammet i figur 13 inneholder 32 brukbare observasjoner (ingen ligger på medianen). Det har én slik for lang run. De 11 månedsverdiene 17-27 ligger alle under medianen for hele perioden, og tilsier at en kan forkaste nullhypotesen om at prosessen er stabil og bare oppviser tilfeldig variasjon omkring en fast medianverdi. I nesten et år etter at selvhjelpsheftet var distribuert, holdt andelen telefonhenvendelser etter kontortid seg lav.
Den andre testen («For mange stigende (eller synkende) observasjoner på rad?») sjekker om tidsserien inneholder noen trend. Igjen er spørsmålet hvor mange som må til for å utgjøre en trend. Carey og Lloyd gir svaret i form av tabell 3.
| Antall brukbare observasjoner | Hva er «for mange stigende (eller synkende) verdier på rad?» |
| 5-8 | 5 eller flere |
| 9-20 | 6 eller flere |
| 21 eller flere | 7 eller flere |
Svaret blir igjen at vi kan forkaste nullhypotesen om at prosessen var stabil gjennom den observerte perioden. For verdiene for de sju påhverandrefølgende månedene 23-29 stiger og stiger. (Hvorfor en ikke skal telle med måned 22, er ikke den starten på stigningen? Nei, den skal ikke telles, for i måned 22 visste en ikke annet enn at verdien for den måneden var lavere enn for måned 21. Først i måned 23 så en en stigning. Derfor er måned 23 den første av den sammenhengende rekka av måneder med stigende verdier.
Begge run-diagram testene konkluderer altså med at en kan forkaste påstanden om at her ser vi en stabil prosess som bare viser tilfeldig variasjon på et stabilt nivå. Det er ikke det som at her ser vi at selvhjelpsheftet hadde den effekt at telefonhenvendelsene etter kontortid ble færre - men at effekten gradvis fortok seg og at antallet slike henvendelser etter hvert steg videre. Spørsmålet om hva det var som gjorde det midlertidige nivåskiftet og skapte trenden må diskuteres for seg - det eneste de to testene viser er at en kan forkaste nullhypotesen om at ikke noe spesielt skjedde.
Kontroll-diagrammer
I den grad det en lurer på er om prosessen har skiftet nivå eller oppviser en trend, trenger en ikke mer for å besvare spørsmålet enn å kunne tegne et run-diagram og gjennomføre de to testene vist over. Og ofte er det nok. Det helt grunnleggende kvalitetsforbedringsspørsmål er om det går bedre eller verre, og det er det samme som å se om her bare er normal variasjon eller om prosessen viser nivåskift eller trend.
Det kan imidlertid hende at en også vil analysere variasjonens størrelse, eller studere enkeltavvik nøyere. Avvik fra normalen kan være interessante selv om de ikke avtegner nivåskift eller trend. De kan f.eks. leses som tegn på at prosessen er dårlig skjermet, og det kan mange ganger være interessant informasjon. I industrien er det nesten alltid viktig. En bildel skal f.eks. ha en bestemt størrelse. Litt vil størrelsen naturligvis variere, for det finnes ikke den maskin eller den prosess som gir på mikrometeren samme resultat hver eneste gang, og små variasjoner kan det være bedre å la være å klå med. Men det er viktig å monitorere variasjonen. Når en ser et stort utslag, er det et signal om at noe uvanlig har slått inn i prosessen. Og når en ser mange utslag av merkbar størrelse kan det bety at nå må maskinen til overhaling og prosessen justeres. Og om en har en variasjon som i og for seg er jevn og ikke inneholder oppsiktsvekkende enkeltutslag, men likevel er større enn konkurrentens, kan det bety at en burde stille strengere toleransekrav til produksjonsprosessen. Variasjonen i produksjonsprosessen kan f.eks. bety at bilkundene og journalistene etter noen år vil bemerke at denne bilen skrangler mer enn andre.
En stor forskjell på produksjonen i industrien og i helsetjenesten er at kliniske prosesser pr definisjon er ustabile. Monitorer en f.eks. intensivpasienters tid på respirator, vil en nødvendigvis se tidsserieplot med variasjon og enkeltutslag som ville fått en bilprodusent til å konkludere at produksjonsprosessen er ute av kontroll. Men i klinikken betyr det som regel ikke prosessfeil. Det er klart at det i blant kommer pasienter som skal ligge 80 døgn på respirator, det er fordi han trenger det, og ellers ville ha dødd - og ikke fordi avdelingen har glemt ham eller fordi prosessen har sviktet på andre måter. Likevel kan det være interessant å studere variasjonen i også helsetjenesteprosesser ved hjelp av kontrolldiagrammer. Et eksempel kan være blodsukkervariasjon: at en diabetiker er velregulert, betyr at variasjonen over tid skal være liten og jo færre ekstremverdier det er, jo bedre er det. Et annet eksempel kan være at epikrisene skal jevnt og trutt være utsendt innen x dager.
Det finnes som sagt mange typer kontrolldiagrammer. En oversikt over typene, og hvordan en velger det som passer best til de data eller den problemstilling en har, finnes f.eks. i Carey og Lloyd (ss 70-77).
I det nedenstående illustrerer jeg bruken av kontrolldigrammer ved to kliniske eksempler a) «Går keisersnittfrekvensen opp?», og b) «Tar det kortere tid enn før å få overvåkingspasientene koplet til monitoreringsutstyret?». Det første eksemplet viser bruken av p-diagram, det andre av XmR-diagram. Begge er hentet fra Carey og Lloyds lærebok, som etter min vurdering er den enkleste og beste innføringsboka om statistisk prosesskontroll i helsetjenesten. Det finnes imidlertid andre: en annen lettlest bok om emnet, som i likhet med Carey og Lloyd også er grundig, er Wheeler DJ, Chambers DS. Understanding Process Control. SPC Press, Knoxville, Tenn. 1992.
Kontrollchart for keisersnittfrekvenser
Ledelsen ved fødeavdelingen blir oppsøkt av en bekymret medarbeider som sier at han tror at nå blir keisersnittene hyppigere. «Prosessen er ute av kontroll» sies det ofte i slike tilfeller. Avdelingssjefen, som naturligvis misliker ikke å ha kontroll, for det er jobben hans å ha det, bestemmer seg for å undersøke saken ved hjelp av statistisk prosesskontroll. Prosenttallene er vist i tabell 7.
| Tabell 7. Antall keisersnitt og antall fødsler i alt i de siste 27 måneder. Fra Carey og Lloyd | ||
| Month |
Number of |
Total Deliveries |
| January 1990 | 65 | 370 |
| February | 64 | 383 |
| March | 77 | 446 |
| April | 59 | 454 |
| May | 64 | 463 |
| June | 74 | 431 |
| July | 72 | 443 |
| August | 67 | 451 |
| September | 59 | 433 |
| October | 65 | 407 |
| November | 60 | 381 |
| December | 68 | 406 |
| January 1991 | 62 | 374 |
| February | 48 | 355 |
| March | 57 | 393 |
| April | 64 | 417 |
| May | 66 | 434 |
| June | 55 | 421 |
| July | 51 | 417 |
| August | 82 | 444 |
| September | 65 | 429 |
| October | 69 | 411 |
| November | 62 | 386 |
| December | 66 | 357 |
| January 1992 | 58 | 373 |
| February | 47 | 370 |
| March | 59 | 415 |
Plottet for 14-månedersperioden er vist i figur 16.
Figur 16. Keiersnittprosenten de siste 12 månedene. Fra Carey & Lloyd, utsnitt av figur 6.15.
Plottet kan tyde på at prosenten går oppover. Her er rett nok ingen trend som er lang nok til å være et signal om prosessendring, men vi ser kanskje et nivåskift?
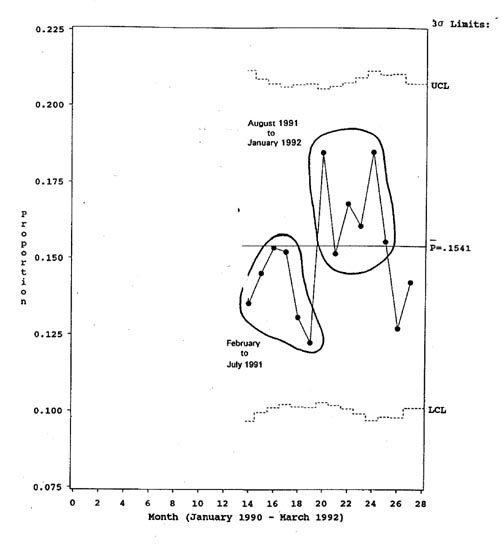
Men så er naturligvis dét at en alltid må velge hvilken periode en skal plotte. Plotter en prosessen så langt bakover som det finnes data, løper en risikoen for å bestemme prosessens stemme ut fra data for helt sikkert ulike perioder. Her, f.eks., har avdelingen bare hatt samme bemanning i 27 måneder, og før det skjedde det mye som kan ha hatt betydning for keisersnittfrekvensen. Derfor plotter avdelingsledelsen tallene for de 27 månedene som prosessen har vær t uendret i, men ikke mer, jfr figur 16.
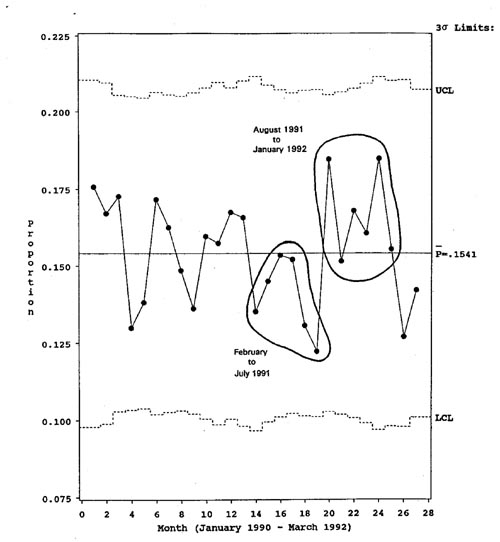
Figur 17. Keisersnittprosenten for 27 måneder. Fra Carey & Lloyd s 125, hele figur 6.15.
Et slikt kontrolldiagram kalles et p-diagram, fordi det baserer seg på gjennomsnittssannsynligheten (p) for at en barselkvinne skulle bli forløst ved keisersnitt. Det viser denne gjennomsnittsprosenten (gjennomsnittet av enkeltmånedenes p-verdier) samt kontrollgrenser som er basert på standardavviket for fordelingen av observerte månedsprosenter.
Den gjennomsnittlige keisersnittprosenten for hele perioden, som er 15,41, sier hvilken keisersnittandel avdelingen gjennomsnittlig må regne med å ha framover, dersom dens obstetriske prosess er stabil, dette er grunntonen i prosessens stemme.
Og så har prosessen øvre og nedre kontrollgrenser. Etter flertallsvedtak blant de statistikere som driver med SPC, ligger kontrollgrensene plussminus 3 standardavvik unna prosessgjennomsnittet. Standardavviket gir et bilde av normalvariasjonen i observasjonsmengden (serien med keisersnittprosenter, måned for måned). De månedene som ligger mer enn tre standardavvik unna gjennomsnittsprosenten for perioden, defineres som så avvikende at de må være uttrykk for at prosessen i den/de måneden(e) må ha vært påvirket av mer enn de vanlige faktorene.
En kan spørre: hvorfor akkurat tre sd, hvorfor ikke to, eller, rettere:1,96 sd - det er jo den grensen som med 5 % sikkerhet identifiserer et avvik fra normalvariasjonen, dvs - i SPC-språket - en «særlig effekt» («special cause variation»)? Svaret er at en i industrien stort sett har funnet at omkostningene ved å gå inn og justere en prosess som det er en femprosentssjanse for at er i orden, er for store. Prosessjustering krever alltid tid og krefter (og sosiale kostnader), og en risiko på 5 % for at endringen bare er klåing, er i flertallets øyne for mye. I industrien vil en tradisjonelt ikke gripe inn for å forbedre en produksjonsprosess før det er minst 99,73 % sikkert at det er noe i veien med den. Ordet «urovekkende» betyr altså i industrien ikke bare «Mer enn 1,96 sd unna gjennomsnittet», det betyr «Mer enn 3 sd unna». Den risiko en i industrien maksimalt vil akseptere for å feilaktig å tro at det er noe galt med en prosess, er altså ikke 5 %, men mye mindre, bare 0,27 %. Men industriens standardsvar er selvsagt ikke riktigere enn andre svar. I industrien er konsekvensene av prosessfeil ikke så nært knyttet til liv og død som i helsetjenesten, så der kan en kanskje tillate seg å vente lenger med å gripe inn i en prosess som en er i tvil om. På den annen side er det også i helsetjenesten noe som heter over-iver. Dessuten er det ikke fra steintavlene vi har regelen om at «det er trygt nok når p er mindre enn 5 %», dvs at kontrollgrensene må være på plussminus 1,96 sd. Også dét er en tommelfingerregel som er vedtatt med knapt flertall. En må alltid velge selv hvilken risiko en vil løpe for å gjøre type 1- og type 2-feil.
Men uansett hvor mange standardavvik ut en vil legge kontrollgrensene som varsler om en bør gripe inn, må en kunne regne ut standardavviket som kontrollgrensene er multipler av. I p-charts følger det av formelen for standardavvik i binomiske fordelinger: sd = ÷[p(1-p)/n], der p er gjennomsnittsandelen keisersnitt for hele den plottete perioden, dvs alle de observerte månedene sett under ett (her: 15,41 %) og n er antallet fødsler i hver måned.
Av denne formelen ser vi forøvrig hvorfor kontrollgrensene i figurene over ikke var tegnet som rette linjer: grunnen er at sd avhenger av n (jfr formelen), og det varierer fra måned til måned hvor mange fødsler avdelingen hadde: lav n gir videre grenser, høy n går trangere grenser.
Av kontrolldiagrammet i figur 16 ser vi at dette er en prosess som er under statistisk kontroll. Observasjonsserien oppviser verken trender eller oppsiktvekkende avvikende enkeltmåneder. Så lenge intet spesielt skjer eller blir gjort, vil en i gjennomsnitt måtte forvente at 15,41 % av forløsningene i denne avdelingen skjer ved keisersnitt, og at en i enkeltmåneder vil kunne ha både langt flere (noe over 20 %) og langt færre (ca 10 % - kan ikke sies endelig, fordi antallet fødsler pr måned svinger (mange fødsler = snevrere kontrollgrenser, få fødsler = videre grenser, med få fødsler skal det med andre ord større avvik i sectioandel til før en kan si statistisk sikkert at her har det skjedd noe uvanlig, at prosessen var ute av kontroll).
XmR-diagram for hvor lang tid det tar å kople opp monitoreringsutstyret for overvåkingspasienter som har vært gjennom en bypassoperasjon til?
Plotter vi pasientene fortløpende med hensyn på hvor mange minutter gikk det faktisk for hver enkelt pasient før alle slanger og ledninger var koplet opp, ser bildet ut som i figur 18.
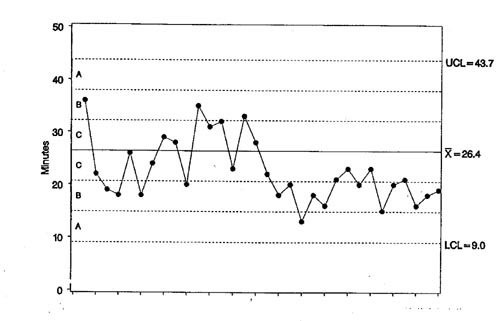
Figur 18. Oppkoplingstid for 32 påhverandrefølgende pasienter i januar (før intervensjonen) og februar (etter intervensjonen). Fra Carey & Lloyd s 106, figur 6.8.
Kontrollgrensene angir grensene for normalvariasjonen i prosessen, verdier utenfor dem er så sjeldne at de antakelig betyr at disse tilfellene er det noe spesielt med. I slike tilfeller bør en vurdere om det bare var vedkommende pasient eller gruppe pasienter som var så annerledes at det måtte være slik, eller om prosessen er uhensiktsmessig konstruert (generelt, eller for denne typen pasienter). I klinikken kan det som sagt ofte være det første. På en av plenumsssamlingene i Gjennombruddsprosjektet Psykiatri viste vi et kontrolldiagram med store utslag - det dreide seg om beltelegging, og vedkommende institusjon hadde høye tall for juli, og mange av deltakerne sa spontant «Aha, så det var hos dere Frederik var den sommeren».
Kontrollgrensene er konstruert ut fra variansen i prosessresultatene. Jo større variansen i prosessen faktisk har vært, jo mer skal til før en vil definere enkeltverdier som oppsiktsvekkende. Vi leter altså etter enkeltpasienter eller pasientsekvenser hvis tilkoplingstid er mer forskjellig fra prosessgjennomsnittet enn prosessens normalvariasjon tilsier. I dette eksemplet ser vi at variasjonen fra pasient til pasient er ganske stor. Det betyr at det skal mye til før en kan si at en pasient er oppsiktvekkende forskjellig, dvs klart mer enn vanlig forskjellig fra de andre pasientene. Kontrolldiagrammet som vi bruker til å analysere dette eksemplet, kalles et XmR-diagram. X betyr at chartet viser de enkelte observasjoner, dvs det antall minutter det tok å kople opp monitoreringsutstyret for hver pasient, mR at det bygger sine kontrollgrenser på prosessens «moving range», dvs på hvor forskjellig (målt i antall minutter) hver pasient var fra pasienten før. Spredningen i observasjonene beregnes som gjennomsnittet av disse forskjellene: jo høyere gjennomsnittsforskjellen er, jo mer forskjellige var pasientene. Kontrollgrensene er multipler av dette gjennomsnittet - og for å si det med en gang: plussminus 2,66 ganger gjennomsnittsforskjellen.
Hvorfor nettopp 2,66, og ikke, f.eks. 1,96. Det korte svaret er: «Av grunner som bare matematikere forstår; tallet kan derfor læres utenat på samme måte som vi har lært at pi er 3,14»: innholdet av en sirkel er 3,14 ganger kvadratet av sirkelradien - bare matematikerne forstår hvorfor, men de har etterprøvd hverandre nok til at vi andre kan stole på det. Det litt lengre svaret, som dog fortsatt invokerer matematikernes troverdighet, er at observasjoner utenfor plussminus 2,66 gjennomsnittsforskjeller er like sjeldne som observasjoner utenfor plussminus 3 sd, slik at også de bare opptrer i 0,27 % av manifesteringene av en stabil prosess.
Figur 18 viser at gjennomsnittstiden for disse pasientene var 26,4 minutter. Forskjellene i tilkoplingstid mellom påhverandrefølgende pasienter (som altså er vårt uttrykk for variasjonen i prosessen) var i gjennomsnitt 6,5 minutter. Kontrollgrensene blir derfor 26,4 minutter plussminus 2,66*6,5 minutter, og det gir en øvre kontrollgrense på 26,4 + 17,3 = 43,7 minutter og en nedre på 26,4 - 17,3 = 9,1 minutter.
(Vi kunne naturligvis brukt samme type kontrolldiagram som over, dvs et p-diagram. Vi kunne jo ha registrert bare hvor stor andel av oppkoplingene hver dag (eller hver uke, om det ikke skjer så mange hver dag) som tok mer enn X (f.eks. 30) minutter - slike måloppnåelseskriterier er ikke så sjeldne. Men vi gjør ikke det: i dette kapitlet er poenget nettopp å presentere to typer kontrolldiagrammer. Det finnes for øvrig enda flere, jfr litteraturen, men en kommer langt med disse to - særlig med dette siste, som alltid lar seg anvende, jfr Wheeler DJ, Chambers DS. Understanding Process Control. SPC Press, Knoxville, Tenn. 1992.
Hadde prosessen vært stabil («i statistisk kontroll»), ville en lest disse tallene slik: i gjennomsnitt vil pasientene som kommer fra bypassoperasjon, trenge 26,4 minutter på å bli tilkoplet alt monitoreringsutstyret. For noen pasienter vil tilkoplingen ta så mye som 43,7 minutter, mens andre vil være klare på 9,1 minutter. 43,7 minutter er ikke et varseltegn, og 9,1 minutter betyr ikke at «nå har de endelig lært hvordan det skal gjøres». Begge verdiene, både den høye (43,7 minutter) og den lave (9,1 minutter) hører til prosessens normalvariasjon. Begge er uttrykk for den samme underliggende arbeidsprosess: etter 43,7 minutter vil det komme kortere perioder, etter 9,1 vil det bli observert lengre. Å belønne teamet som klarte det på 9,1 minutter, er å berede grunnen for senere å bli ekstra skuffet over nettopp disse medarbeiderne («Hvordan kunne de bli så slappe, endatil etter at jeg hadde gitt dem en konferansereise i belønning! Neimen om de skal lure meg til å gi slik belønning en annen gang!»). Å refse de som brukte 43,7 minutter er også feil (med mindre en vet noe annet om arbeidet enn det som framkommer av kontrollchartet).
Konklusjonen blir at denne prosessen ikke er i statistisk kontroll. Den viser en forbedring: det tar kortere tid etter hvert. Kontrollgrensene i diagrammet er nettopp konstruert for å undersøke om en intervensjon har hatt effekt. Her er gjennomført et forsøk som siktet mot å gjøre tilkoplingene raskere. Diagrammet viser tilkoplingstidene for 16 pasienter før forbedringsforsøket og 16 etter. Og kontrollgrensene er utregnet på grunnlag av tall for de 16 preintervensjonstilfellene. For: når en er ute etter å se hvordan resultatene fra den endrete prosessen legger seg i forhold til den opprinnelige prosessens stemme, må en sørge for å ha identifisert den først. Så kan en i neste omgang bestemme den endrete prosessens stemme, og lete etter to ting: a) om grunntonen har forandret seg i ønsket retning, og b) om den tilfeldige variasjonen er blitt mindre (dvs om plussminus 2,66*gjennomsnitts-forskjellen mellom hver pasient og den neste definerer et smalere intervall enn før).
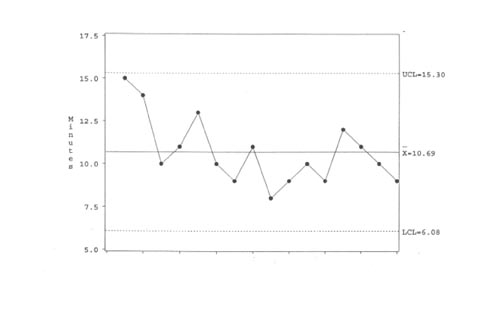
Figur 19 viser tydelig at det er tilfellet her.
Figur 19. Oppkoplingstid for 16 påhverandrefølgende pasienter i april. Fra Carey & Lloyd s 106, figur 6.10.
Den endrete prosessen har en kapabilitet, utregnet etter tilkoplingstiden for 16 pasienter i april, som kan beskrives slik: gjennomsnittstiden er redusert til 10,7 minutter, gjennomsnittsforskjellen fra pasient til pasient er nede på 1,7 minutter, og intervallet mellom kontrollgrensene er såpass trangt som fra en øvre grense på 10,7 + 2,66*1,7 = 10,7 + 4,5 = 15,2 minutter til en nedre på 10,7 - 4,5 = 6,2 minutter.
Forbedring med og uten statistisk prosesskontroll
Over har jeg argumentert for at tidsserieanalyser i form av statistisk prosesskontroll er nyttig, og vist ved noen eksempler hvordan en på den måten fortere enn ved tradisjonelle sammenlikninger av før- og etter-verdier kan få statistisk sikre svar på spørsmålet om det går bedre eller verre.
Avslutningsvis vil jeg likevel gjenta at en naturligvis kan drive vellykket forbedringsarbeid også uten å gjøre bruk av statistisk prosesskontroll. Mange av avdelingene som deltok i Gjennombruddsprosjektet Psykiatri har vist det. Selv om flere av avdelingene i dette gjennombruddsprosjektet enn i de forrige har laget tidsserieplott, er de fortsatt et mindretall. Og mange av dem som ikke har brukt slike monitorerings- og analyseteknikker rapporterer om gode resultater. Fra utprøvingsjournalene og sluttrapportene laget til prosjektets siste samling, Forbedringssseminar 3 i Tromsø 11-13 juni 2001, fra en avdeling som ikke brukte slike teknikker, kan f.eks. hitsettes, vilkårlig utvalgt blant de mange som meldte om gode resultater: «... har effektivisert utredning og tidsbruk, noe som nær har halvert liggetiden på tvungen observasjon. Når vi i tillegg har vist at disse pasientene sjelden overføres til videre tvungent psykisk helsevern vil denne reduksjonen [...] innebære en betydelig reduksjon av tvangsbruk.» En annen enhet rapporterte slik: «Vår hovedmålsetting var nådd allerede i 2. periode, nemlig en reduksjon på mer enn 25 %. Tallene for periode 3 viste at antallet liggedøgn på tvang var redusert med ca 34 %, dette er betydelig mer enn vi hadde antatt. Vi ser også at trenden holder seg i 4. periode - en reduksjon på 35 % totalt. Vi er overrasket over at vi har kunnet få til en så markant endring med klart avgrenset, overkommelig innsats!». Og fra en tredje meldtes: «Det vi har oppnådd med dette prosjektet er at antall innleggelser etter §3-6 er redusert med 50 % sammenlignet med samme periode i fjor [...] til tross for at det har vært 50 flere innleggelser i år sammenlignet med samme periode i fjor».
Litteratur:
Carey, R. G. and Lloyd R. C.: Measuring Quality Improvement in Health Care. Milwaukee, Wisconsin: Quality Press 2001.
Wheele r DJ, Chambers DS. Understanding Process Control. SPC Press, Knoxville, Tenn. 1992.